
 繁体
繁体
卷四十八志二十三(2/6)
次均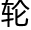 半径一十一万七千五百。
半径一十一万七千五百。
黄白大距半较九分三十秒。
均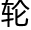 半径二十九万。
半径二十九万。
月孛应三 0四度四十九分五十四秒0九微。
0四度四十九分五十四秒0九微。
正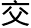 每日平行一百九十秒,小馀六四。
每日平行一百九十秒,小馀六四。
太 平行应一
平行应一 0八度四十分五十七秒十六微。
0八度四十分五十七秒十六微。
求初实行,置用时太 平行,减去月孛行,得引数。用平三角形,以本
平行,减去月孛行,得引数。用平三角形,以本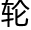 半径之半为对正角之边,以引数为一角,求得对角之边三因之。又求得对又一角之边,与本天半径相加减。引数九
半径之半为对正角之边,以引数为一角,求得对角之边三因之。又求得对又一角之边,与本天半径相加减。引数九 至二
至二 相加,三
相加,三 至八
至八 相减。复用平三角形,以三因数为小边,加减本天半径数为大边,正角在两边之中,求得对小边之角为初均数,求得对正角之边。即次
相减。复用平三角形,以三因数为小边,加减本天半径数为大边,正角在两边之中,求得对小边之角为初均数,求得对正角之边。即次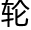 最近
最近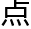 距地心之线。乃置用时太
距地心之线。乃置用时太 平行,以初均数加减之,引数初
平行,以初均数加减之,引数初 至五
至五 为减,六
为减,六 以后为加。为初实行。
以后为加。为初实行。
求用时太 平行,以本日太
平行,以本日太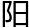 均数变时,详日躔。得均数时差。均数加者,时差为减;均数减者,时差为加。又以本日太
均数变时,详日躔。得均数时差。均数加者,时差为减;均数减者,时差为加。又以本日太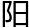 黄、赤经度详日躔。相减馀数变时,得升度时差。二分后为加,二至后为减。乃以两时差相加减,为时差总。两时差加减同号者,则相加为总,加者仍为加,减者仍为减。加减异号者,则相减为总,加数大者为加,减数大者为减。化秒,与太
黄、赤经度详日躔。相减馀数变时,得升度时差。二分后为加,二至后为减。乃以两时差相加减,为时差总。两时差加减同号者,则相加为总,加者仍为加,减者仍为减。加减异号者,则相减为总,加数大者为加,减数大者为减。化秒,与太 每时平行相乘为实,以一度化秒为法除之,得数为秒,以度分收之,得时差行。以加减太
每时平行相乘为实,以一度化秒为法除之,得数为秒,以度分收之,得时差行。以加减太 平行,时差总为加者则减,减者则加。为用时太
平行,时差总为加者则减,减者则加。为用时太 平行。
平行。
太 每日平行四万七千四百三十五秒,小馀0二一一七七。
每日平行四万七千四百三十五秒,小馀0二一一七七。
求正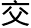 平行,以积日与正
平行,以积日与正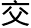 每日平行相乘,满周天秒数去之,馀数收为
每日平行相乘,满周天秒数去之,馀数收为 度分,以减正
度分,以减正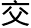 应,正
应,正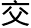 应不足减者,加十二
应不足减者,加十二 减之。得正
减之。得正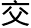 年
年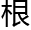 。上考则加。又置正
。上考则加。又置正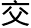 每日平行,以距天正冬至次日数乘之,得数为秒,以
每日平行,以距天正冬至次日数乘之,得数为秒,以 度分收之,以减年
度分收之,以减年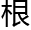 ,年
,年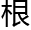 不足减者,加十二
不足减者,加十二 减之。为正
减之。为正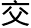 平行。
平行。
本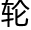 半径五十八万。
半径五十八万。
朔、望黄白大距四度五十八分三十秒。
推月离法求天正冬至,同日躔。
月孛即最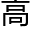 ,每日行四百0一秒,小馀0七七四七七。
,每日行四百0一秒,小馀0七七四七七。
负圈半径七十九万七千。
正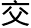 应六
应六 二十七度十三分三十七秒四十八微。
二十七度十三分三十七秒四十八微。
次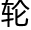 半径二十一万七千。
半径二十一万七千。
月离用数
黄白大距中数五度0八分。
求白 实行,置初实行,减本日太
实行,置初实行,减本日太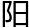 实行得次引。即距日度。用平三角形,以次
实行得次引。即距日度。用平三角形,以次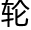 最近
最近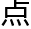 距地心线为一边,倍次引之通弦本天半径为一率,次引之正弦为二率,次
距地心线为一边,倍次引之通弦本天半径为一率,次引之正弦为二率,次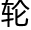 半径为三率,求得四率倍之即通弦。为一边;以初均数与引数减半周之度引数不及半周,则与半周相减,如过半周,则
半径为三率,求得四率倍之即通弦。为一边;以初均数与引数减半周之度引数不及半周,则与半周相减,如过半周,则
求太 平行,置中积分,加气应详日躔。小馀,不用日,下同。减天正冬至小馀,得积日。上考则减气应小馀,加天正冬至小馀。与太
平行,置中积分,加气应详日躔。小馀,不用日,下同。减天正冬至小馀,得积日。上考则减气应小馀,加天正冬至小馀。与太 每日平行相乘,满周天秒数去之,馀数收为
每日平行相乘,满周天秒数去之,馀数收为 度分。以加太
度分。以加太 平行应,得太
平行应,得太 年
年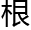 。上考则减,又置太
。上考则减,又置太 每日平行,以距天正冬至次日数乘之,得数为秒。以
每日平行,以距天正冬至次日数乘之,得数为秒。以 度分收之,与年
度分收之,与年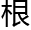 相并,满十二
相并,满十二 去之。为太
去之。为太 平行。
平行。
正切。检表得度,与黄 相减,馀变时为升度时差。二分后为加,二至后为减。皆加减节气时刻,为节气用时。求距纬度,以本天半径为一率,黄赤大距度之正弦为二率,实行距
相减,馀变时为升度时差。二分后为加,二至后为减。皆加减节气时刻,为节气用时。求距纬度,以本天半径为一率,黄赤大距度之正弦为二率,实行距 秋分前后度之正弦为三率,实行初
秋分前后度之正弦为三率,实行初 初度至二
初度至二 末度,与三
末度,与三 相减,馀为
相减,馀为 分前;三
分前;三 初度至五
初度至五 末度,则减去三
末度,则减去三 ,为
,为 分后。六
分后。六 初度至八
初度至八 末度,与九
末度,与九 相减,馀为秋分前;九
相减,馀为秋分前;九 初度至十一
初度至十一 末度,则减去九
末度,则减去九 ,为秋分后。求得四率为正弦,检表得距纬度。实行三
,为秋分后。求得四率为正弦,检表得距纬度。实行三 至八
至八 ,其纬在赤
,其纬在赤 北;九
北;九 至二
至二 ,其纬在赤
,其纬在赤 南。
南。
太 每时四刻。平行一千九百七十六秒,小馀四五九二一五七。
每时四刻。平行一千九百七十六秒,小馀四五九二一五七。
两弦黄白大距五度一十七分三十秒。
求日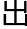
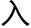 昼夜时刻,以本天半径为一率,北极
昼夜时刻,以本天半径为一率,北极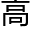 度之正切为二率,本日距纬度之正切为三率,求得四率为正弦,检表得日
度之正切为二率,本日距纬度之正切为三率,求得四率为正弦,检表得日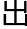
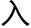 在卯酉前后赤
在卯酉前后赤 度。变时,一度变时之四分,凡言变时皆仿此。为距卯酉分。以加减卯酉时,即得日
度。变时,一度变时之四分,凡言变时皆仿此。为距卯酉分。以加减卯酉时,即得日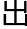
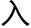 时刻。
时刻。 分前、秋分后,以加卯正为日
分前、秋分后,以加卯正为日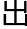 ,减酉正为日
,减酉正为日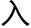 。
。 分后、秋分前,以减卯正为日
分后、秋分前,以减卯正为日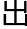 ,加酉正为日
,加酉正为日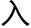 。又倍距卯酉分,以加减半昼分,得昼夜时刻。
。又倍距卯酉分,以加减半昼分,得昼夜时刻。 分后以加得昼刻,以减得夜刻,秋分后反是。
分后以加得昼刻,以减得夜刻,秋分后反是。
求月孛行,以积日见前条,下同。与月孛每日行相乘,满周天秒数去之,馀数收为 度分。以加月孛应,得月孛年
度分。以加月孛应,得月孛年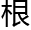 。上考则减。又置月孛每日行以距天正冬至次日数乘之,得数为秒,以
。上考则减。又置月孛每日行以距天正冬至次日数乘之,得数为秒,以 度分收之,与年
度分收之,与年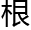 相并,满十二
相并,满十二 去之。为月孛行。
去之。为月孛行。