
 繁体
繁体
卷四十九志二十四(2/6)
求太 半径,以太
半径,以太 最
最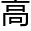 距地为一率,地半径比例数为二率,太
距地为一率,地半径比例数为二率,太 距地心线内减去次均
距地心线内减去次均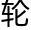 半径为三率,求得四率为太
半径为三率,求得四率为太 距地。又以太
距地。又以太 距地为一率,太
距地为一率,太 实半径为二率,本天半径为三率,求得四率为正弦。检表得太
实半径为二率,本天半径为三率,求得四率为正弦。检表得太 半径。
半径。
求黄 地平
地平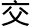 角,以
角,以 甚时刻变赤
甚时刻变赤 度,每时之四分变一度。又于太
度,每时之四分变一度。又于太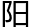 赤
赤 经度内减三
经度内减三 ,不及减者,加十二
,不及减者,加十二 减之。馀为太
减之。馀为太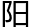 距
距 分赤
分赤 度。两数相加,满全周去之。为
度。两数相加,满全周去之。为 分距
分距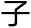 正赤
正赤 度。与半周相减,得
度。与半周相减,得 分距午正东西赤
分距午正东西赤 度。过半周者,减去半周,为午正西。不及半周者,去减半周,为午正东。
度。过半周者,减去半周,为午正西。不及半周者,去减半周,为午正东。 分距午正东西度过象限者,与半周相减,馀为秋分距午正东西赤
分距午正东西度过象限者,与半周相减,馀为秋分距午正东西赤 度。秋分距午东西,与
度。秋分距午东西,与 分相反。以
分相反。以 秋分距午正东西度与九十度相减,馀为
秋分距午正东西度与九十度相减,馀为 秋分距地平赤
秋分距地平赤 度。乃用为弧三角形之一边,以黄赤大距及赤
度。乃用为弧三角形之一边,以黄赤大距及赤 地平
地平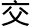 角即赤
角即赤 地平上
地平上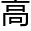 度,
度, 分午西、
分午西、
求太 赤
赤 经纬度,详月离求太
经纬度,详月离求太
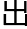
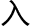 时刻条。
时刻条。
求实望用时,以日实均变时为均数时差,以升度差黄赤 经度之较。变时为升度时差,两时差相加减为时差总,加减之法,详月离求用时平行条。以加减实望,为实望用时。距日
经度之较。变时为升度时差,两时差相加减为时差总,加减之法,详月离求用时平行条。以加减实望,为实望用时。距日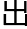 后日
后日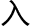 前九刻以内者,可以见
前九刻以内者,可以见 。九刻以外者全在昼,不必算。
。九刻以外者全在昼,不必算。
求 分,以太
分,以太 全径为一率,十分为二率,并径太
全径为一率,十分为二率,并径太 地影两半径相并。内减
地影两半径相并。内减 甚距纬之较并径不及减距纬即不
甚距纬之较并径不及减距纬即不 。为三率,求得四率即
。为三率,求得四率即 分。
分。
求 既、生光时刻,以
既、生光时刻,以 甚距纬之馀弦为一率,两半径较之馀弦为二率,半径千万为三率,求得四率为馀弦,检表得
甚距纬之馀弦为一率,两半径较之馀弦为二率,半径千万为三率,求得四率为馀弦,检表得 既、生光距弧。又以月距日实行化秒为一率,一小时化秒为二率,
既、生光距弧。又以月距日实行化秒为一率,一小时化秒为二率, 既、生光距弧化秒为三率,求得四率为秒。以时分收之,为
既、生光距弧化秒为三率,求得四率为秒。以时分收之,为 既、生光距时。以加减
既、生光距时。以加减 甚时刻,得
甚时刻,得 既、生光时刻。减得
既、生光时刻。减得 既,加得生光。
既,加得生光。
求 甚距纬,以本天半径为一率,黄白大距之正弦为二率,实
甚距纬,以本天半径为一率,黄白大距之正弦为二率,实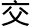 周之正弦为三率,求得四率为正弦,检表得
周之正弦为三率,求得四率为正弦,检表得 甚距纬。实
甚距纬。实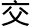 周初
周初 五
五 为北,六
为北,六 十一
十一 为南。
为南。
求太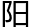 黄赤
黄赤 实经度,以一小时化秒为一率,太
实经度,以一小时化秒为一率,太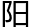 一小时平行为二率,实距时化秒为三率,求得四率为秒,以度分收之,为太
一小时平行为二率,实距时化秒为三率,求得四率为秒,以度分收之,为太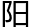 距弧。依时距时加减号。以加减太
距弧。依时距时加减号。以加减太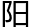 平行,又以日实均加减之,即黄
平行,又以日实均加减之,即黄 经度。又用弧三角形求得赤
经度。又用弧三角形求得赤 经度。详月离求太
经度。详月离求太
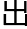
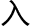 时刻条。
时刻条。
为三率,求得四率为秒,以度分收之,为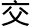 周距弧。以加减太
周距弧。以加减太
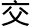 周,依实距时加减号。又以月实均加减之,为实
周,依实距时加减号。又以月实均加减之,为实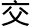 周。若实
周。若实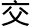 周
周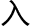 必
必 之限,为有
之限,为有 。自五
。自五 十七度四十三分0五秒至六
十七度四十三分0五秒至六 十二度十六分五十五秒,自十一
十二度十六分五十五秒,自十一 十七度四十三分0五秒至初
十七度四十三分0五秒至初 十二度十六分五十五秒,为必
十二度十六分五十五秒,为必 之限。不
之限。不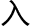 此限者,不必布算。
此限者,不必布算。
求 限总时,以初亏、复圆距时倍之,即得。
限总时,以初亏、复圆距时倍之,即得。
求太 黄
黄 经纬度,置太
经纬度,置太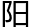 黄
黄 经度,加减六
经度,加减六 ,过六
,过六 则减去六
则减去六 ,不及六
,不及六 ,则加六
,则加六 。再加减
。再加减 甚距弧,又加减黄白升度差,求升度差法,详月离求黄
甚距弧,又加减黄白升度差,求升度差法,详月离求黄 实行条。得太
实行条。得太 黄
黄 经度。求纬度,详月离。
经度。求纬度,详月离。
求初亏、复圆时刻,以 甚距纬之馀弦为一率,并径之馀弦为二率,半径千万为三率,求得四率为馀弦,检表得初亏、复圆距弧。又以月距日实行化秒为一率,一小时化秒为二率,初亏、复圆距弧化秒为三率,求得四率为秒。以时分收之,为初亏、复圆距时。以加减
甚距纬之馀弦为一率,并径之馀弦为二率,半径千万为三率,求得四率为馀弦,检表得初亏、复圆距弧。又以月距日实行化秒为一率,一小时化秒为二率,初亏、复圆距弧化秒为三率,求得四率为秒。以时分收之,为初亏、复圆距时。以加减 甚时刻,得初亏、复圆时刻。减得初亏,加得复圆。
甚时刻,得初亏、复圆时刻。减得初亏,加得复圆。
求 甚时刻,以本天半径为一率,黄白大距之馀弦为二率,实
甚时刻,以本天半径为一率,黄白大距之馀弦为二率,实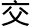 周之正切为三率,求得四率为正切,检表得
周之正切为三率,求得四率为正切,检表得 甚
甚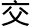 周。与实
周。与实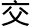 周相减,为
周相减,为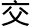 周升度差。又以太
周升度差。又以太 一小时引数与太
一小时引数与太 实引相加,依月离求初均法算之,为后均。以后均与月实均相加减,两均同号相减,异号相加。得数又与一小时月距日平行相加减,两均同加,后均大则加,小则减。两均同减,后均大则减,小则加。两均一加一减,其加减从后均。为月距日实行。乃以月距日实行化秒为一率,一小时化秒为二率,
实引相加,依月离求初均法算之,为后均。以后均与月实均相加减,两均同号相减,异号相加。得数又与一小时月距日平行相加减,两均同加,后均大则加,小则减。两均同减,后均大则减,小则加。两均一加一减,其加减从后均。为月距日实行。乃以月距日实行化秒为一率,一小时化秒为二率,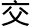 周升度差化秒为三率,求得四率为秒。以时分收之,得
周升度差化秒为三率,求得四率为秒。以时分收之,得 甚距时。以加减实望用时,实
甚距时。以加减实望用时,实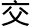 周初
周初 六
六 为减,五
为减,五 十一
十一 为加。为
为加。为 甚时刻。
甚时刻。
求地影半径,以太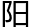 最
最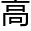 距地为一率,地半径比例数为二率,太
距地为一率,地半径比例数为二率,太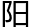 距地心线为三率,求得四率为太
距地心线为三率,求得四率为太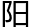 距地。又以太
距地。又以太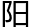 光分半径内减地半径为一率,太
光分半径内减地半径为一率,太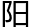 距地为二率,地半径为三率,求得四率为地影之长。又以地影长为一率,地半径为二率,本天半径为三率,求得四率为正弦,检表得地影角。又以本天半径为一率,地影角之正切为二率,地影长内减太
距地为二率,地半径为三率,求得四率为地影之长。又以地影长为一率,地半径为二率,本天半径为三率,求得四率为正弦,检表得地影角。又以本天半径为一率,地影角之正切为二率,地影长内减太 距地为三率,求得四率为太
距地为三率,求得四率为太 所
所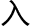 地影之阔。乃以太
地影之阔。乃以太 距地为一率,地影之阔为二率,本天半径为三率,求得四率为正切,检表得地影半径。
距地为一率,地影之阔为二率,本天半径为三率,求得四率为正切,检表得地影半径。
求宿度,同日躔。