
 繁体
繁体
卷五十二志二十七(2/6)
图形尚无资料
图形尚无资料
推算太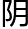 凌犯视差,固依后编求日
凌犯视差,固依后编求日 三差之法,而其为用不同。盖日
三差之法,而其为用不同。盖日 之东西差为求视距弧,而南北差为求视纬,其视距弧、视纬则为求视相距及视行之用。缘太
之东西差为求视距弧,而南北差为求视纬,其视距弧、视纬则为求视相距及视行之用。缘太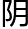 行于白
行于白 ,是必以白平象限为准焉。若五星之距恆星、五星之互相距,皆以黄
,是必以白平象限为准焉。若五星之距恆星、五星之互相距,皆以黄 同经度之时为相距时刻,而较黄纬南北相距之数为其上下之分也。至月距五星、月距恆星,亦皆以黄
同经度之时为相距时刻,而较黄纬南北相距之数为其上下之分也。至月距五星、月距恆星,亦皆以黄 经度相同之时为凌犯时刻,不更问白
经度相同之时为凌犯时刻,不更问白 经度,其于白平象限又何与焉?然其以东西差定视时之
经度,其于白平象限又何与焉?然其以东西差定视时之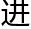 退,以南北差判视纬之大小,以定视距之远近者,其差皆黄
退,以南北差判视纬之大小,以定视距之远近者,其差皆黄 经纬之差,故必以黄平象限之
经纬之差,故必以黄平象限之 度为准。黄平象限者,地平上黄
度为准。黄平象限者,地平上黄 半周適中之
半周適中之 也。顾黄
也。顾黄 与赤
与赤 斜
斜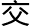 ,地平上赤
,地平上赤 半周適中之
半周適中之 ,恆当
,恆当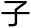 午圈,而地平上黄
午圈,而地平上黄 半周適中之
半周適中之 ,则时有更易。盖黄极由负黄极圈每日随天左旋,绕赤极一周,如黄极在赤极之南,则冬至当午正,其黄
,则时有更易。盖黄极由负黄极圈每日随天左旋,绕赤极一周,如黄极在赤极之南,则冬至当午正,其黄 斜升斜降;若黄极在赤极之北,则夏至当午正,其黄
斜升斜降;若黄极在赤极之北,则夏至当午正,其黄 正升正降,而黄平象限亦皆恰当
正升正降,而黄平象限亦皆恰当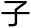 午圈;设黄极在赤极之西,则
午圈;设黄极在赤极之西,则 分当午正,其黄
分当午正,其黄 之势斜倚,
之势斜倚,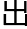 自东北而
自东北而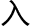 西南,黄平象限乃在午正之东;设黄极在赤极之东,则秋分当午正,其黄
西南,黄平象限乃在午正之东;设黄极在赤极之东,则秋分当午正,其黄
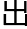 自东南而
自东南而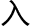 西北,黄平象限乃在午正之西。是则黄
西北,黄平象限乃在午正之西。是则黄 之向,随时不同,故以黄
之向,随时不同,故以黄 之逐度,推求黄平象限及限距地
之逐度,推求黄平象限及限距地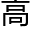 以立表。
以立表。
四率戊辰弧正切
二率戊角馀弦
图形尚无资料
,即赤 上应加之升度时差。其时差一为加、一为减,而两数相等,乃减尽无馀,既无时差之总数,则其凌犯时刻即为用时可知矣。此法以丑
上应加之升度时差。其时差一为加、一为减,而两数相等,乃减尽无馀,既无时差之总数,则其凌犯时刻即为用时可知矣。此法以丑 凌犯时刻减去均数时差,得未
凌犯时刻减去均数时差,得未 实行虚映之时刻,而复加相等之升度时差,所得用时,固仍在丑
实行虚映之时刻,而复加相等之升度时差,所得用时,固仍在丑 之位,盖因太
之位,盖因太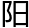 平行距
平行距 分后黄
分后黄 度等于太
度等于太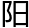 实行距
实行距 分后赤
分后赤 度故也。又如太
度故也。又如太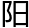 正当本天之最卑或最
正当本天之最卑或最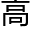 ,乃无平行实行之差,自无均数时差,止加减升度时差一数。设太
,乃无平行实行之差,自无均数时差,止加减升度时差一数。设太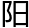 当本天最卑,又当
当本天最卑,又当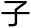 正,如太
正,如太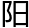 在黄
在黄 之
之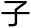
 ,则庚乙与庚
,则庚乙与庚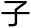 等,以庚丑
等,以庚丑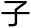 正弧形求得丑乙黄赤升度差。变时减于乙
正弧形求得丑乙黄赤升度差。变时减于乙 时刻,即得丑
时刻,即得丑 用时,乃在乙
用时,乃在乙
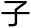 正之前也。若太
正之前也。若太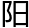 当本天最
当本天最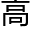 ,又当午正,如太
,又当午正,如太 在黄
在黄 之午
之午 ,则壬丁与壬午等,以壬寅午正弧形求得寅丁黄赤升度差,变时减于丁
,则壬丁与壬午等,以壬寅午正弧形求得寅丁黄赤升度差,变时减于丁 时刻,即得寅
时刻,即得寅 用时,乃在丁
用时,乃在丁 午正之前也。
午正之前也。
一率半径
三率戊甲弧正切
四率甲辰弧正弦
又如太 实行正当冬、夏至或正当
实行正当冬、夏至或正当 、秋分,此四
、秋分,此四 皆无黄
皆无黄 赤
赤 之差,自无升度时差,止加减均数时差一数。设太
之差,自无升度时差,止加减均数时差一数。设太 实行六
实行六 初度为正当夏至,在黄
初度为正当夏至,在黄 之辛
之辛 ,当赤
,当赤 于戊,而平行卯
于戊,而平行卯 ,当赤
,当赤 于辰,自卯
于辰,自卯 与丙甲戊过极至经圈平行作卯午距等圈,则午
与丙甲戊过极至经圈平行作卯午距等圈,则午 为凌犯时刻,其戊午与辛卯均数等,变时得均数时差。减于午
为凌犯时刻,其戊午与辛卯均数等,变时得均数时差。减于午 而得戊
而得戊 ,即用时也。
,即用时也。
一率半径
求 分距午时分、黄平象限
分距午时分、黄平象限 度及限距地
度及限距地
二率戊角正弦
三率戊甲弧正弦
又设太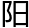 正当秋分
正当秋分 ,黄
,黄 实行为九
实行为九 初度,求午正初刻
初度,求午正初刻 分距午时分并黄平象限及限距地
分距午时分并黄平象限及限距地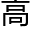 ,即以秋分当于正午之戊,则庚未戊为黄
,即以秋分当于正午之戊,则庚未戊为黄 ,
,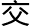 地平于寅,庚为
地平于寅,庚为 分,未为夏至,
分,未为夏至,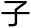 乙未己为过极至经圈,亦自黄极
乙未己为过极至经圈,亦自黄极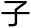

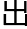 弧过天
弧过天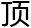 ,作
,作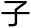 甲卯弧黄平象限,
甲卯弧黄平象限,
先设太 正当
正当 分
分 ,黄
,黄 实行为三
实行为三 初度,求午正初刻黄平象限
初度,求午正初刻黄平象限 度及限距地
度及限距地 度分。如图甲乙丙丁为
度分。如图甲乙丙丁为 午圈,甲为天
午圈,甲为天 ,丙丁为地平,乙为北极,乙丙为京师北极
,丙丁为地平,乙为北极,乙丙为京师北极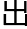 地,
地,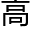 三十九度五十五分,戊己庚为赤
三十九度五十五分,戊己庚为赤 ,
,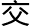 于地平之己
于地平之己 ,其戊
,其戊 当午正,为地平上赤
当午正,为地平上赤 半周適中之
半周適中之 ,戊丁为赤
,戊丁为赤 距地
距地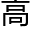 五十度五分,当戊己丁角,辛
五十度五分,当戊己丁角,辛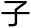 壬为负黄极圈,
壬为负黄极圈,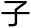 为黄极,乙
为黄极,乙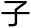 己丑为过极至经圈,戊丑庚为黄
己丑为过极至经圈,戊丑庚为黄 ,而
,而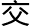 地平于寅
地平于寅 ,庚为秋分,丑为冬至,戊为
,庚为秋分,丑为冬至,戊为 分,即太
分,即太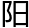 之所在,临于午正,乃无
之所在,临于午正,乃无 分距午之时分。试自黄极
分距午之时分。试自黄极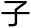

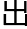 弧线过天
弧线过天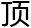 作
作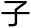 甲卯黄
甲卯黄 经圈,为本时黄平象限,其辰
经圈,为本时黄平象限,其辰 为地平上黄
为地平上黄 半周適中之
半周適中之 ,而在正午之东,即黄平象限
,而在正午之东,即黄平象限 度也。辰寅卯角为黄
度也。辰寅卯角为黄 与地平相
与地平相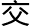 之角,而当辰卯弧,即本时限距地
之角,而当辰卯弧,即本时限距地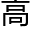 之度也。法用戊辰甲正弧三角形求戊辰、甲辰二弧,此形有辰直角,有戊甲弧赤
之度也。法用戊辰甲正弧三角形求戊辰、甲辰二弧,此形有辰直角,有戊甲弧赤 距天
距天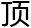 ,与乙丙北极
,与乙丙北极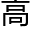 度等。以赤
度等。以赤
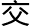
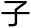 午圈之戊直角九十度内减己戊丑角黄赤
午圈之戊直角九十度内减己戊丑角黄赤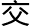 角二十三度二十九分,得寅戊丁角六十六度三十一,为黄
角二十三度二十九分,得寅戊丁角六十六度三十一,为黄
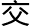
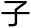 午圈角;亦名黄
午圈角;亦名黄 赤经
赤经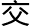 角。与辰戊甲角为对角,其度等。乃以半径为一率,戊角黄
角。与辰戊甲角为对角,其度等。乃以半径为一率,戊角黄 赤经
赤经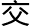 角之馀弦为二率,戊甲弧赤
角之馀弦为二率,戊甲弧赤 距天
距天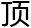 ,亦即太
,亦即太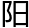 距天
距天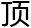 其正切为三率,求得四率,为黄平象限距午之正切,检表得十八度二十六分十四秒,为戊辰弧黄平象限距午正之黄
其正切为三率,求得四率,为黄平象限距午之正切,检表得十八度二十六分十四秒,为戊辰弧黄平象限距午正之黄 度。与戊
度。与戊
 分三
分三 相加,因黄平象限在午东,故加。得辰
相加,因黄平象限在午东,故加。得辰 三
三 十八度二十六分十四秒,即本时黄平象限之经度也。又以半径为一率,戊角黄
十八度二十六分十四秒,即本时黄平象限之经度也。又以半径为一率,戊角黄 赤经
赤经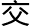 角之正弦为二率,戊甲弧太
角之正弦为二率,戊甲弧太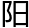 距天
距天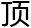 之正弦为三率,求得四率,为黄平象限距天
之正弦为三率,求得四率,为黄平象限距天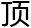 之正弦,检表得三十六度三分九秒,为甲辰弧黄平象限距天
之正弦,检表得三十六度三分九秒,为甲辰弧黄平象限距天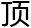 。与甲卯象限九十度相减,得辰卯弧五十三度五十六分五十一秒,即本时限距地
。与甲卯象限九十度相减,得辰卯弧五十三度五十六分五十一秒,即本时限距地 ,而当辰寅卯角之度也。
,而当辰寅卯角之度也。