
 繁体
繁体
卷二十二(2/7)
九
 初月度:(《乾元》谓之月离
初月度:(《乾元》谓之月离
 九
九 正
正 月度、九
月度、九 朔度。《仪天》谓之求月离正
朔度。《仪天》谓之求月离正 九
九 宿度。)置月离
宿度。)置月离 初黄
初黄 宿度,各以所
宿度,各以所 限数乘之,(遇半倍使)如百而一,为泛差;用求黄、赤二
限数乘之,(遇半倍使)如百而一,为泛差;用求黄、赤二 差,依前法加减之,即月离
差,依前法加减之,即月离 初九
初九 宿度。(《乾元》以日躔
宿度。(《乾元》以日躔
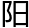 差
差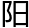 加
加 减,为朔、望常分;又以所
减,为朔、望常分;又以所 限率乘,正
限率乘,正 黄
黄 宿度相从之,以求黄、赤二
宿度相从之,以求黄、赤二 差,如前加减,为月离正
差,如前加减,为月离正 九
九 宿度;以
宿度;以
 定度加而命之,即朔月离宿度。《仪天》置正
定度加而命之,即朔月离宿度。《仪天》置正 月离黄
月离黄 ,以距度下月九
,以距度下月九 差,宗法乘之,以距度所
差,宗法乘之,以距度所 限数乘度,余从之,为总差;半而退位,一百一收之,又计冬、夏二至以求度数乘,满九十而一为度差,依前法加减,为正
限数乘度,余从之,为总差;半而退位,一百一收之,又计冬、夏二至以求度数乘,满九十而一为度差,依前法加减,为正 月离九
月离九 。)
。)
求九 朔月度:百约月离先后定数,后加先减四十二,用减中盈而从朔日,乃加
朔月度:百约月离先后定数,后加先减四十二,用减中盈而从朔日,乃加 初九
初九 宿次,即得所求。(《乾元》置九
宿次,即得所求。(《乾元》置九 正
正 之度及分,以
之度及分,以
 定度加之,命以九
定度加之,命以九 宿次,即其朔加时月离宿度及分也。《仪天》法见下。《乾元》又有定
宿次,即其朔加时月离宿度及分也。《仪天》法见下。《乾元》又有定 度,置月离
度,置月离
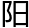 定数,以七十一乘之,满九百一除之为分,用
定数,以七十一乘之,满九百一除之为分,用 减
减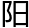 加常分为度及分。)
加常分为度及分。)
求九 望月度:(《仪天》谓之求定朔、望加时日月度。)以象积加朔九
望月度:(《仪天》谓之求定朔、望加时日月度。)以象积加朔九 月度,命以其
月度,命以其 ,即得所求。(《乾元》置朔、望加时日相距之度,以天中度及分加之,为加时象积;用加九
,即得所求。(《乾元》置朔、望加时日相距之度,以天中度及分加之,为加时象积;用加九 朔月度,命以其
朔月度,命以其 宿次去之,即望日月度及分也。自望推朔亦如之。《仪天》求定朔望加时九
宿次去之,即望日月度及分也。自望推朔亦如之。《仪天》求定朔望加时九 日度,以其朔、望去
日度,以其朔、望去 度,
度, 前者减之,
前者减之, 后者加之,满九
后者加之,满九 宿度去之,即定朔、望加时九
宿度去之,即定朔、望加时九 日度也。求定朔望加时九
日度也。求定朔望加时九 月度,置其日加时九
月度,置其日加时九 日度,其
日度,其
朱 ;(
;( 分、秋分后,朱
分、秋分后,朱 半
半 在夏至之宿,
在夏至之宿, 黄
黄 南;立
南;立 、立秋后,朱
、立秋后,朱 半
半 在立夏之宿,
在立夏之宿, 黄
黄 西南:至所冲之宿亦如之。)
西南:至所冲之宿亦如之。) 在
在 历,秋在
历,秋在 历,月行黑
历,月行黑 。(
。( 分、秋分后,黑
分、秋分后,黑 半
半 在冬至之宿,
在冬至之宿, 黄
黄 北;立
北;立 、立秋后,黑
、立秋后,黑 半
半 在立冬之宿,
在立冬之宿, 黄
黄 东北:至所冲之宿亦如之。)四序月离为八节,九
东北:至所冲之宿亦如之。)四序月离为八节,九 斜正不同,所
斜正不同,所 七十二候,皆与黄
七十二候,皆与黄 相会。各距
相会。各距 初黄
初黄 宿度,每五度为限。初限十二,每限减半,终九限又减尽,距二立之宿减一度少
宿度,每五度为限。初限十二,每限减半,终九限又减尽,距二立之宿减一度少 ,却从减尽起,每限减半,九限终十二而至半
,却从减尽起,每限减半,九限终十二而至半 ,乃去黄
,乃去黄 六度;又自十二,每限减半,终九限又减一度少
六度;又自十二,每限减半,终九限又减一度少 ,更从减尽起,每限增半,九限终十二,复与日轨相会。
,更从减尽起,每限增半,九限终十二,复与日轨相会。 初、
初、 中、半
中、半 ,各以限数,遇半倍使,乘限度为泛差。其
,各以限数,遇半倍使,乘限度为泛差。其 中前后各九限,以距二至之宿前后候数乘之,半
中前后各九限,以距二至之宿前后候数乘之,半 前后各九限,各至二分之宿前后候数乘之,皆满百而一为黄
前后各九限,各至二分之宿前后候数乘之,皆满百而一为黄 差。在冬至之宿后,
差。在冬至之宿后, 初前后各九限为减,
初前后各九限为减, 中前后各九限为加;夏至之宿后,
中前后各九限为加;夏至之宿后, 初前后各九限为加,
初前后各九限为加, 中前后各九限为减。大凡月
中前后各九限为减。大凡月 后为
后为 黄
黄 外,
外, 中后为
中后为 黄
黄 内。半
内。半 前后各九限,在
前后各九限,在 分之宿后
分之宿后 黄
黄 外,秋分之宿后
外,秋分之宿后 黄
黄 内,皆以差为加;在
内,皆以差为加;在 分之宿后
分之宿后 黄
黄 内,秋分之宿后
内,秋分之宿后 黄
黄 外,皆以差为减。倍泛差,退一位,(遇减,
外,皆以差为减。倍泛差,退一位,(遇减, 外除三;遇加,
外除三;遇加, 外除一。)又以黄
外除一。)又以黄 差减,为赤
差减,为赤 差。
差。 初、
初、 中前后各九限,以差加;半
中前后各九限,以差加;半 前后各九限,皆以差减。以黄赤
前后各九限,皆以差减。以黄赤 差减黄
差减黄 宿度为九
宿度为九 宿度,有余分就近收为太、半、少之数。(《乾元》初数九,每限减一,终于一,限数并同,即八十四除之。《仪天》初数一百一十七,每限减一十,终于二十七,以一百一除。二历皆不
宿度,有余分就近收为太、半、少之数。(《乾元》初数九,每限减一,终于一,限数并同,即八十四除之。《仪天》初数一百一十七,每限减一十,终于二十七,以一百一除。二历皆不 外为法。初中正
外为法。初中正 、
、 秋二分、冬夏二至前后各九限,加减并同《应天》。又《仪天》即除法是九十乘黄
秋二分、冬夏二至前后各九限,加减并同《应天》。又《仪天》即除法是九十乘黄 泛差,一百一收为度,乃得月与黄、赤
泛差,一百一收为度,乃得月与黄、赤 定差。以上
定差。以上
 定月
定月
 各六度相较之差,黄
各六度相较之差,黄 随其日行所向,斜正各异,余皆同《应天》。《仪天》有求定朔望加时
随其日行所向,斜正各异,余皆同《应天》。《仪天》有求定朔望加时 迟疾历初末限,置经朔、望
迟疾历初末限,置经朔、望 迟疾初末限日及余秒,如求定朔、弦、望法
迟疾初末限日及余秒,如求定朔、弦、望法 之,即各得所求。又求初中正
之,即各得所求。又求初中正
 历,置其朔、望加时
历,置其朔、望加时 迟疾历初末限日及余秒,视其日月行
迟疾历初末限日及余秒,视其日月行

 历日及余秒,如近前
历日及余秒,如近前 者即加,近后
者即加,近后 者即返减
者即返减 中日余,乃如之,各得初、中、正
中日余,乃如之,各得初、中、正
 迟疾历初末限日及余秒也。其加减满或不足,即
迟疾历初末限日及余秒也。其加减满或不足,即 退象限及余秒,各得所求。又求朔望加时及初、中、正
退象限及余秒,各得所求。又求朔望加时及初、中、正
 迟疾限日
迟疾限日 历积度,各置小余,以其日历定分乘之,宗法收之为分,一百一除之为度,以加其日下历积度,各得所求。又《乾元》、《仪天》有求正
历积度,各置小余,以其日历定分乘之,宗法收之为分,一百一除之为度,以加其日下历积度,各得所求。又《乾元》、《仪天》有求正 黄
黄 月度,《乾元》元率通定
月度,《乾元》元率通定 度及分,以一百二十七乘之,满九十五而一,
度及分,以一百二十七乘之,满九十五而一, 一等,复收为
一等,复收为
 度,用减其朔加时日度,即朔前月离正
度,用减其朔加时日度,即朔前月离正 黄
黄 宿度。《仪天》置朔、望及正
宿度。《仪天》置朔、望及正 历积度,以少减多,余为月行去
历积度,以少减多,余为月行去 度及分;乃视其朔望在
度及分;乃视其朔望在 前者加、
前者加、 后者减朔望加时黄
后者减朔望加时黄 月度,为初、中、正
月度,为初、中、正 黄
黄 月度也。)
月度也。)