
 繁体
繁体
卷五十一志二十六(2/6)
求天正冬至,
求各省月 时刻方位,理同甲
时刻方位,理同甲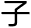 元法。
元法。
推日 法
法
求实朔用时,与月 求实望用时同。比视日
求实望用时同。比视日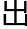
 ,同甲
,同甲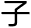 元法。
元法。
绘月 图,同甲
图,同甲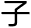 元法。
元法。
求太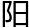 太
太 实引,
实引,
求初亏、复圆并径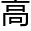 弧
弧 角,以并径为一率,
角,以并径为一率, 甚实纬为二率,半径千万为三率,求得四率为馀弦,检表为并径
甚实纬为二率,半径千万为三率,求得四率为馀弦,检表为并径 实纬角。如无
实纬角。如无 甚实纬,即无此角,亦无并径黄
甚实纬,即无此角,亦无并径黄
 角。又置九十度,加减斜距黄
角。又置九十度,加减斜距黄
 角,得初亏、复圆黄
角,得初亏、复圆黄
 实纬角。
实纬角。 甚月距正
甚月距正 初
初 、六
、六 ,初亏减,复圆加。五
,初亏减,复圆加。五 、十一
、十一 ,初亏加,复圆减。各与并径
,初亏加,复圆减。各与并径 实纬角相减,为初亏、复圆并径黄
实纬角相减,为初亏、复圆并径黄
 角。并径初
角。并径初 实纬角小,距纬南北与
实纬角小,距纬南北与 甚同。大则反是。以加减黄
甚同。大则反是。以加减黄
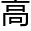 弧
弧 角,亏限东,复圆限西,纬南加,纬北减。初亏限西,复圆限东,加减反是。各得并径
角,亏限东,复圆限西,纬南加,纬北减。初亏限西,复圆限东,加减反是。各得并径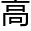 弧
弧 角。如无并径黄
角。如无并径黄
 角,则黄
角,则黄
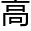 弧
弧 角即并径
角即并径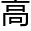 弧
弧 角。
角。
求 甚太
甚太 赤
赤 经纬宿度,以半径千万为一率,
经纬宿度,以半径千万为一率, 甚太
甚太 距
距 、秋分黄
、秋分黄 经度正弦为二率,
经度正弦为二率, 甚太
甚太 黄
黄 经度不及三
经度不及三 者,与三
者,与三 相减;过三
相减;过三 者,减三
者,减三 ;过六
;过六 者,与九
者,与九 相减;过九
相减;过九 者,减九
者,减九 。
。 甚太
甚太 黄
黄 纬度馀切为三率,求得四率为馀切,检表得太
纬度馀切为三率,求得四率为馀切,检表得太 距二分弧与黄
距二分弧与黄
 角,以加减黄赤大距,
角,以加减黄赤大距, 甚太
甚太 黄
黄 经度九
经度九 至三
至三 ,纬南加,纬北减,皆在赤
,纬南加,纬北减,皆在赤 南,反减则在北。三
南,反减则在北。三 至九
至九 加减反是。为太
加减反是。为太 距二分弧与赤
距二分弧与赤
 角。又以太
角。又以太 距二分弧与黄
距二分弧与黄
 角之馀弦为一率,半径千万为二率,
角之馀弦为一率,半径千万为二率, 甚太
甚太 距
距 、秋分黄
、秋分黄 经度之正切为三率,求得四率,为太
经度之正切为三率,求得四率,为太 距二分弧之正切。又以半径千万为一率,太
距二分弧之正切。又以半径千万为一率,太 距二分弧与赤
距二分弧与赤
 角之馀弦为二率,太
角之馀弦为二率,太 距二分弧正切为三率,求得四率为正切,检表为距
距二分弧正切为三率,求得四率为正切,检表为距 、秋分赤
、秋分赤 经度。加减三
经度。加减三 九
九 ,
, 甚太
甚太 黄
黄 经度不及三
经度不及三 ,与三
,与三 相减,过三
相减,过三 者加三
者加三 。过六
。过六 者,与九
者,与九 相减,过九
相减,过九 者加九
者加九 。得
。得 甚太
甚太 赤
赤 经度。求纬度宿度,同甲
经度。求纬度宿度,同甲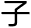 元法。
元法。
日 用数
用数
求 甚太
甚太
求太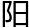 实半径,先求太
实半径,先求太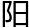 视半径,法同月
视半径,法同月 。内减太
。内减太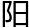 光分,得太
光分,得太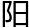 实半径。
实半径。
求带 分秒,用两经斜距,不用月距日实行,馀与甲
分秒,用两经斜距,不用月距日实行,馀与甲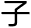 元法同。
元法同。
求平朔,
求太

 限,并同月
限,并同月 ,惟不用望策,即为逐月朔太
,惟不用望策,即为逐月朔太
 周。视某月
周。视某月 可
可 之限,即为有
之限,即为有 之月。
之月。 周自五
周自五 八度四十二分至六
八度四十二分至六 九度一十四分,又自十一
九度一十四分,又自十一 二十度四十六分至初
二十度四十六分至初 二十一度一十八分,皆可
二十一度一十八分,皆可 之限。
之限。
太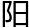 光分一十五秒,馀见日躔、月离、月
光分一十五秒,馀见日躔、月离、月 。
。
求纪日,
。得 甚太
甚太 白
白 经度。又置实望月距正
经度。又置实望月距正 ,加减距时月实行,得
,加减距时月实行,得 甚月距正
甚月距正 。再求黄
。再求黄 经纬宿度,同月离。
经纬宿度,同月离。
求初亏、复圆方位,即以并径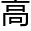 弧
弧 角为定
角为定 角,求法同甲
角,求法同甲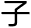 元。但以并径
元。但以并径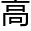 弧
弧 角初度初亏在限东为正下,限西为正上;复圆在限东为正上,限西为正下。据京师北极
角初度初亏在限东为正下,限西为正上;复圆在限东为正上,限西为正下。据京师北极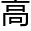 度定,与甲
度定,与甲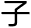 元法同。
元法同。
求地平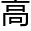 下差,先求本日太
下差,先求本日太 最大地半径差,法同月
最大地半径差,法同月 。乃减太
。乃减太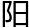 最大地半径差,得地平
最大地半径差,得地平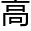 下差。
下差。
求带 方位,用带
方位,用带 两心相距,不用并径求诸
两心相距,不用并径求诸 角,如初亏、复圆定方位。
角,如初亏、复圆定方位。 甚前与初亏同,
甚前与初亏同, 甚后与复圆同。
甚后与复圆同。
求太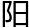 太
太 距地,并同月
距地,并同月 。
。
求初亏、复圆黄
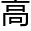 弧
弧 角,以半径千万为一率,黄赤大距正弦为二率,影距
角,以半径千万为一率,黄赤大距正弦为二率,影距 、秋分黄
、秋分黄 经度正弦为三率,求得四率为正弦,检表得影距赤
经度正弦为三率,求得四率为正弦,检表得影距赤 度。影距
度。影距 、秋分度数与太
、秋分度数与太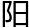 同,太
同,太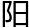 在赤
在赤 北,影在南,太
北,影在南,太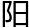 在赤
在赤 南,影在北。又以影距
南,影在北。又以影距 、秋分黄
、秋分黄 经度馀弦为一率,黄赤大距馀切为二率,半径千万为三率,求得四率为正切,检表为黄
经度馀弦为一率,黄赤大距馀切为二率,半径千万为三率,求得四率为正切,检表为黄 赤经
赤经 角。乃用弧三角形,以北极距天
角。乃用弧三角形,以北极距天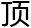 为一边,影距赤
为一边,影距赤 与九十度相加减为一边,北则减,南则加。初亏、复圆各
与九十度相加减为一边,北则减,南则加。初亏、复圆各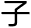 正时刻过十二时者,与二十四时相减。变赤
正时刻过十二时者,与二十四时相减。变赤 度,各为所夹之角,求得对北极距天
度,各为所夹之角,求得对北极距天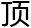 之角。各为赤经
之角。各为赤经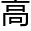 弧
弧 角,以加减黄
角,以加减黄 赤经
赤经 角,太
角,太 在夏至前六
在夏至前六 ,
, 在
在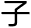 正后则减,为限西。
正后则减,为限西。 在
在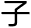 正前则加,加过九十度,与半周相减,为限东。不及九十度,则不与半周相减,变为限西。在夏至后六
正前则加,加过九十度,与半周相减,为限东。不及九十度,则不与半周相减,变为限西。在夏至后六 反是。各得黄
反是。各得黄
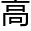 弧
弧 角。若
角。若 在
在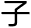 正,影在正午,无赤经
正,影在正午,无赤经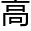 弧
弧 角,则黄
角,则黄 赤经
赤经 角即黄
角即黄
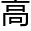 弧
弧 角。太
角。太 在夏至前为限西,后为限东。
在夏至前为限西,后为限东。
求 甚用时,与月
甚用时,与月 求
求 甚时刻法同。
甚时刻法同。
求实朔实时,并同月 求望法,惟不加望策。视本时月距正
求望法,惟不加望策。视本时月距正

 限为有
限为有 。自五
。自五 十一度三十四分至六
十一度三十四分至六 六度二十二分,又自十一
六度二十二分,又自十一 二十三度三十八分至初
二十三度三十八分至初 十八度二十六分,为有
十八度二十六分,为有 之限。
之限。
求太 视半径,法同月
视半径,法同月 。
。
求首朔,